实习和秋招 计算机基础

线性表、栈、队列和数组

数据结构中除了串、树和图之外的知识。

Posted by Sunny on 2024-11-09
Words 3.3k and Reading Time 12 Minutes
Viewed Times

线性表、栈、队列和数组

写在前面：其实这些内容应该写成几篇文章，但由于是秋招复习，我就把这些比较基础的数据结构放到一篇文章里，还有利于我们进行对比记忆！那么我们就开始吧！

首先，线性表、栈、队列和数组都属于数据的逻辑结构范畴，但是逻辑结构在计算机中的存储和本身逻辑结构无关。一种逻辑结构可以有多种存储结构的实现方法。比如逻辑结构线性表的存储结构有——顺序存储和链式存储。

其次，这四种逻辑结构的内在逻辑是——线性表是最基础的存在，栈、队列和数组都是特殊的线性表。其中，栈和队列是操作受限的线性表，

线性表(Linear List)

线性表是具有相同数据类型的$n$个数据元素的有限序列。

线性表的几个我认为比较重要的特点：

  • 数据元素个数有限
  • 数据元素在逻辑上有顺序性
  • 每个数据元素占有相同大小的存储空间

线性表的存储结构

线性表的存储结构分为两种——顺序存储和链式存储。

线性表的顺序存储

线性表的顺序存储又称为顺序表。它是用一组地址连续的存储单元依次存储线性表中的数据元素，从而使得逻辑上相邻的两个元素在物理位置上也相邻。实现了逻辑结构和存储结构的统一。

高级程序设计语言通常用数组来描述线性表的顺序存储结构。

顺序表的优点：

  • 可以进行随机访问，访问顺序表中的元素时间复杂度为$O(1)$。
  • 存储密度高，每个结点只存储数据元素（无需存储指针）。

顺序表的缺点：

  • 插入和删除需要移动大量元素。插入操作平均移动$n/2$个元素，删除操作平均移动$(n-1)/2$个元素。
  • 灵活性差，每次都需要分配一段连续的存储空间。

顺序表的基本操作

重点分析几种基本操作移动结点的平均次数。

  1. 插入操作：如果在顺序表第$0$位置插入元素，需要移动$n$个元素；如果在顺序表的末尾插入元素，需要移动$0$个元素，时间复杂度用$O(1)$表示；所以平均移动次数为$\sum_{i=0}^n p_i(n-i)={n \over 2}$，插入元素算法的时间复杂度为$O(n)$。
  2. 删除操作：如果删除第一个元素，需要移动$n-1$个元素；如果删除末尾元素，需要移动$0$个元素；平均移动元素数量是$\sum_{i=0}^{n-1} p_i(n-i-1)={n-1 \over 2}$。
  3. 按值查找（顺序查找）：如果目标元素是第一个元素，需要比较$1$次，时间复杂度可以表示为$O(1)$；如果目标元素是末尾元素，需要比较$n$次；平均比较次数是$\sum_{i=0}^n p_i(n-i+1)={n+1 \over 2}$。

顺序表插入、删除和按值查找算法时间复杂度均为$O(n)$。

线性表的链式存储

线性表的链式存储又称为链表。链表的内容可以分为单链表、双链表、循环链表（循环单链表和循环双链表）和静态链表。

单链表

通过一组任意的存储单元来存储线性表中的数据元素，使用指针建立数据元素之间的线性关系。对于每个链表结点，同时保存元素自身信息和一个指向后继数据元素结点的指针。

通常使用头指针(head)来标识一个单链表，指向单链表的起始地址。需要讨论head是否为NULL，如果head==NULL，说明单链表是空的，否则指向单链表的第一个结点。

单链表的重要操作

  1. 插入结点操作

插入结点可以分为前插和后插。后插操作的时间复杂度为$O(1)$。前插操作可以转换为后插操作，并且将传统前插操作的时间复杂度$O(n)$降为$O(1)$。

前插=后插 + 交换待插入结点$s$和目标结点$p$的data域。

1
2
3
4
5
6
7
//后插
s->next = p->next;
p->next = s;
//交换值
temp = s->data;
s->data = p->data;
p->data = temp;

  1. 删除结点操作

删除某个特定结点$p$，如果按照传统操作，需要先找到结点的前驱结点，再进行删除操作，此时时间复杂度为$O(n)$。如果将问题转化为删除$p$的下一个结点，并将下一个结点的data域赋给$*p$，时间复杂度可以将为$O(1)$。

1
2
3
4
q = p->next;
p->data = p->next->data;
p->next = p->next->next;
free(q);

  1. 建立单链表：有头插法和尾插法两种，为了保持数据元素顺序，推荐使用尾插法。

双链表

对于每个链表结点，同时保存元素自身信息、一个指向后继数据元素结点的指针以及一个指向前驱元素结点的指针。

循环链表

循环单链表和单链表的区别是，最后一个结点的后继指针不是指向NULL，而是指向链表的第一个结点。

循环双链表和双链表的区别是，最后一个结点的后继指针指向第一个结点，并且第一个结点的前驱指针指向最后一个结点。

静态链表

静态链表是使用数组来描述线性表的链式存储结构，静态链表需要一块连续的内存空间保存。对于每一个结点，也有数据域和指针域，指针域是下一个结点在数组中的相对地址。下面这张图可以很轻松地理解静态链表了：

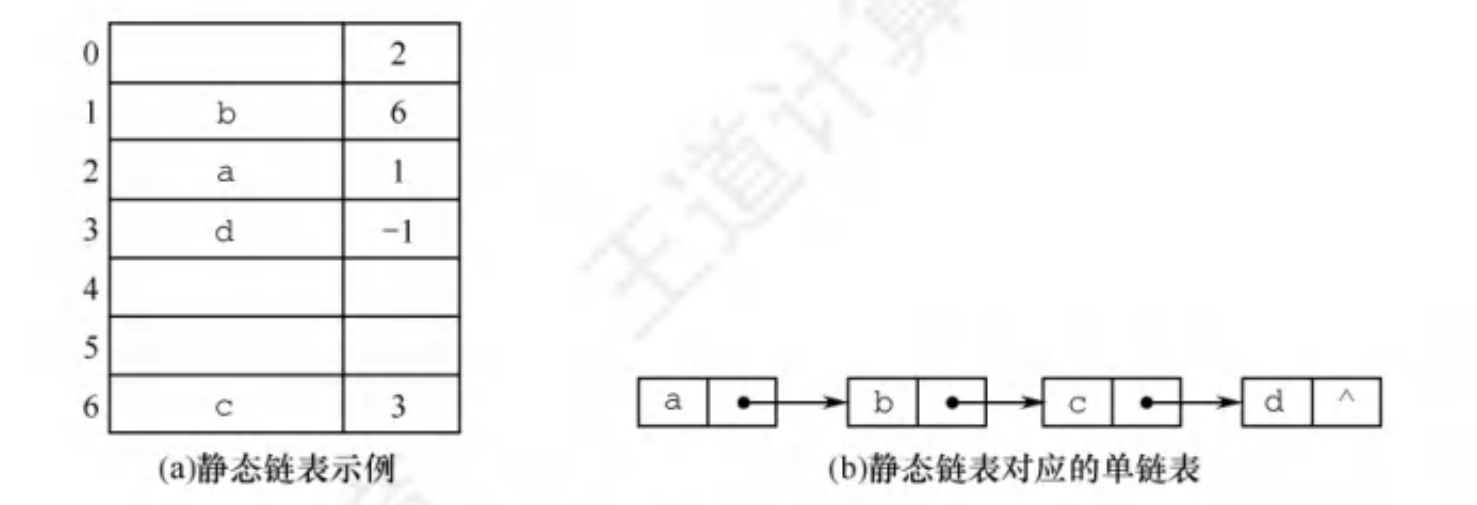
顺序表和链表的比较

区别

  1. 存取方式：顺序表可以顺序存取也可以随机存取，但是链表只能顺序存取。
  2. 逻辑结构和物理结构：线性表在逻辑结构和物理结构保持统一，但是链表逻辑结构相邻，物理结构不一定相邻。
  3. 查找、插入和删除：链表的查询算法复杂度均为$O(n)$。无序线性表按值查询时间复杂度为$O(n)$；有序线性表按值查找可以使用折半查找，时间复杂度为$O(\log_2n)$；线性表按序号查找时间复杂度均为$O(1)$。对于插入和删除操作，线性表平均要移动半个表长的元素，链表只需要修改相关结点的指针域即可。
  4. 空间分配：线性表存储密度高（因为不用考虑指针域），但是线性表的规模需要提前确定（因为需要分配连续的空间）。链表在需要添加新的结点时，为新结点申请空间即可，更加灵活。

如何选择线性表还是链表？

可以从存储，运算（复杂度），环境的方向进行思考。

栈(Stack)

栈是只允许在一端进行插入或删除操作的线性表。栈有两个新的概念：栈顶(Top)、栈底(Bottom)。

因为栈的本质是一种操作受限制的线性表，所以栈也有顺序和链式两种存储结构。

栈的顺序存储结构

采用顺序存储的栈称为顺序栈，顺序栈利用一组地址连续的存储单元按照从栈底到栈顶的顺序存在数据元素，同时设一个指针(Top)指示当前栈顶元素的位置。

初始化，设置栈顶指针$Top=-1$；进栈时，先$Top=Top+1$，再送值到栈顶；出栈时，先取栈顶元素，然后$Top=Top-1$。

共享栈：让两个顺序栈共享一个一维数组空间。将一个栈底设置为$-1$，另一个栈底设置为$Maxsize$。

栈的链式存储结构

采用链式存储的栈称为链栈。

队列(Queue)

队列是只允许在表的一端进行插入，而在表的另一端进行删除的线性表。操作特性采用先进先出的原则，即先入队的元素先出队。

队有两个新概念，队头(Front)指允许删除的一端，队尾(Rear)指允许插入的一端。（其实这两个可以交换，但我个人偏好这样设置）

队列的顺序存储

队列的顺序存储是指分配一块连续的存储空间存放队列中的元素，设队列为$Q$，队首指针为$Q.front$，队尾指针为$Q.rear$。

初始化，$Q.front=Q.rear=0$；新元素入队：将元素送至队尾，再$Q.rear=Q.rear+1$；元素出队：先取队首元素值，再$Q.front=Q.front+1$。

循环队列

顺序队列会存在假溢出的问题，由于$Q.front$和$Q.rear$n不断增长，所以可以使用循环队列解决上述问题。我们将顺序队列想象成一个环。循环队列在传统顺序队列基础上，所有操作在计算时需要$\%Maxsize$。

初始化，$Q.front=Q.rear=0$；新元素入队：将元素送至队尾，再$Q.rear=(Q.rear+1)\%Maxsize$；元素出队：先取队首元素值，再$Q.front=(Q.front+1)\%Maxsize$；计算队列长度$(Q.rear+Maxsize-Q.front)\%Maxsize$。

队列的链式存储

队列的链式表示称为链队列，本质上是一个带有队头指针和队尾指针的单链表。

双端队列

双端队列是指允许两端都可以进行插入和删除操作的线性表。

个人感觉栈和队列的内容需要配合王道练习题理解。

数组(Array)

定义：数组是由$n$($n\geq 1$)个相同类型的数据元素构成的有限序列，每个数据元素都是一个数组元素。

  • 下标：每个元素在n个线性关系中的序号。
  • 维界：下标的取值范围。

数组是线性表的推广。一维数组可视为一个线性表；二维数组可视为其元素是定长数组的线性表。数组一旦被定义，其维数和维界就不再改变。

数组的存储结构

一个数组的所有元素在内存中占有一段连续的存储空间。

以一维数组$A[0…n-1]$为例，其存储结构关系式为:

其中，$L$是每个数据元素所占的存储单位。

特殊矩阵的压缩存储

目的是节省存储空间，提升性能。

对称矩阵

主要考察对角矩阵压缩存储的下标对印关系。

由于对称矩阵上三角区和下三角区元素是一致的，所以会浪费一半存储空间。所以我们只需要存储下三角区和主对角线的元素，即$a_{i,j}(i \geq j)$。我们将$n$阶对接矩阵$A$存放在一维数组$B[n(n+1)/2]$中。

元素$a_{i,j}$在数组中的下标是$k=1+2+…+(i-1)+j-1={i(i-1)\over 2}+j-1$。

元素下标之间的对应关系如下：

三角矩阵

下三角矩阵是上三角区的所有元素均为同一常量。（上三角矩阵同理）下三角区和主对角线元素按顺序存储，紧接着存储上三角区的常量，所以将$n$阶下三角矩阵$A$压缩存储在$B[n(n+1)/2+1]$。

下三角矩阵元素下标之间的对应关系为（从$0$开始）：

上三角矩阵元素下标的对应关系为（从$0$开始）：

三对角矩阵

对角矩阵也称带状矩阵。对$n$阶矩阵$A$中的任意一个元素$a{i,j}$，当$|i-j|>1$时，都有$a{i,j}=0$，则称为三对角矩阵。按照行优先方式存放在数组中，下标$k=2i+j-3$。

稀疏矩阵

矩阵中的非零元素的个数$t$，相对于矩阵元素的个数$s$来说非常少，则称为这种矩阵为稀疏矩阵。可以采用三元组(行标$i$，列标$j$，值$a_{i,j}$)的形式保存稀疏矩阵。

应用

个人感觉，应用这部分更加重要，更贴近对计算机的理解以及编程题刷题。

栈的应用

括号匹配

表达式求值

递归

队列的应用

层次遍历

计算机系统

FEATURED TAGS
实习和秋招 计算机基础
FRIENDS